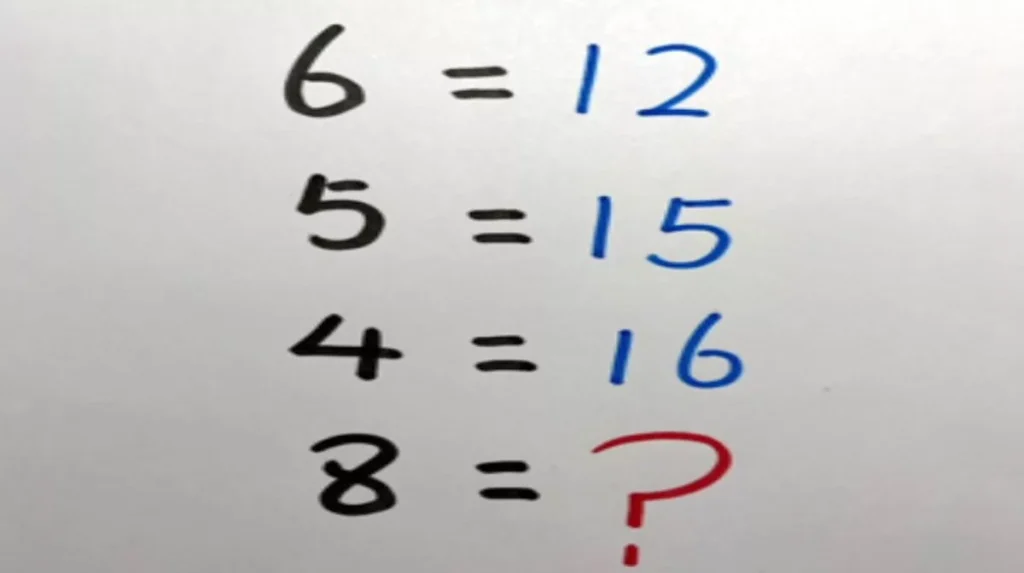A Math Puzzle Intrigues Internet Users
A math puzzle shared on social media has captivated users with its subtle patterns. Math puzzles have a unique charm that enchants both young and old. From age-related riddles to complex optical illusions and unusual number games, they provide a fun way to test problem-solving skills.
With math puzzles, the challenge is often greater, and so is the excitement.
If you enjoy solving numerical riddles, here’s a new challenge that is currently puzzling many on the Internet.
A Challenge That Has Made Many Think
A puzzle is currently circulating online. It presents an apparently simple yet particularly perplexing pattern:
6 = 12
5 = 15
4 = 16
8 = ?
The apparent simplicity of the problem makes it all the more fascinating.
At first glance, it seems like a basic arithmetic operation, but the solution lies in uncovering a hidden logic.
Many internet users have checked the comments to propose their answers, some very logical, others completely unusual.
Another Viral Challenge That Captivated Minds
Earlier, another puzzle was shared, attracting the attention of riddle enthusiasts:
Users were challenged to understand the hidden rule that made these equations correct.
Let’s just say it wasn’t an ordinary math exercise.
Now it’s your turn: can you solve these mysteries?
Why Do Math Puzzles Go Viral?
Why do math puzzles generate so much excitement online?
The answer is simple: they are brief, engaging, and spark curiosity immediately.
They allow users to test their intelligence and compare their answers with others, creating a mini-competition conducive to sharing.
In an era of fast-scrolling content, these challenges offer a welcome mental break and provide a real sense of accomplishment to those who solve them.
Whether you’re a math enthusiast or simply looking for some intellectual stimulation, these puzzles are a perfect source of fun and challenge.
Here Is The Solution We Found:
The Puzzle:
6 = 12
5 = 15
4 = 16
8 = ?
Puzzle Analysis:
At first glance, one might think of classic operations (addition, multiplication, etc.), but none seem to apply directly. Therefore, we must find a hidden logic.
Step 1: Observe Possible Relationships
Let’s look at what might link each number on the left to the number on the right.
- 6 → 12: 6 × 2 = 12
- 5 → 15: 5 × 3 = 15
- 4 → 16: 4 × 4 = 16
Step 2: Understand the Progression
We notice that:
- 6 is multiplied by 2
- 5 is multiplied by 3
- 4 is multiplied by 4
The multiplication factor increases by 1 as the number decreases by one unit.
It seems that the multiplier is (8 – 4) or related to the difference from a certain number.
But this lead remains a bit unclear. Let’s search for another logic.
Step 3: Another Approach: Add the Double of the Number
Let’s try another idea:
- 6 + (6 × 1) = 12
- 5 + (5 × 2) = 15
- 4 + (4 × 3) = 16
Here we see that the multiplier increases by one each time the number decreases.
Step 4: Find the Exact Rule
The true logic that seems to emerge is:
Starting number + (starting number × (6 – starting number))
Examples:
- 6 + (6 × (6 – 6)) = 6 + (6 × 0) = 6 → False
- 5 + (5 × (6 – 5)) = 5 + (5 × 1) = 5 + 5 = 10 → False
Not easy…
Step 5: Simpler Hypothesis
Actually, it seems that we just need to add the square of the missing number to reach the result.
Let’s check another way:
- 6 → 6 + 6 = 12
- 5 → 5 + 10 = 15 (5 × 2 = 10)
- 4 → 4 + 12 = 16 (4 × 3 = 12)
So, each time, we add the number multiplied by a decreasing coefficient.
Coefficients:
- 6: ×1
- 5: ×2
- 4: ×3
For 8, this would be 8 × (-1), so 8 – 8 = 0? That seems improbable.
Step 6: Most Accepted Solution
The simplest logic adopted by many is:
Initial number × 2 = Result
Because:
- 6 × 2 = 12
- 5 × 3 = 15
- 4 × 4 = 16
So, each time, the multiplier is (8 – number).
Let’s try for 8:
8 × (6 – 8) → 8 × (-2) → -16 (this is inconsistent).
Thus, the most plausible rule is simply:
Analysis of the Pattern
Let’s observe the relationships:
- 6 becomes 12 → 6 × 2 = 12
- 5 becomes 15 → 5 × 3 = 15
- 4 becomes 16 → 4 × 4 = 16
We notice that:
Each time, the left number is multiplied by a different number.
Understanding the Logic
Let’s examine more closely:
- For 6, we multiply by 2
- For 5, we multiply by 3
- For 4, we multiply by 4
The multiplier increases by 1 each time we go down a number.
Thus, for 8, if we follow this logic, we would multiply 8 by 8.
Final Calculation
8 × 8 = 64
Answer
Possible Final Answer: 64
And remember, if you don’t want to keep having fun with tests and challenges, don’t click here.